John Von Neumann:  Genius of Man and Machine

John Von Neumann, one of this century’s preeminent scientists, along with being a great mathematician and physicist, was an early pioneer in fields such as game theory, nuclear deterrence, and modern computing.  His was a mind comfortable in the realms of both man and machine.  His kinship with the logical machine was displayed at an early age by his ability to compute the product of two eight-digit numbers in his head.  His strong and lasting influence on the human world is apparent through his many friends and admirers who so often had comments as to Von Neumann’s greatness as a man and a scientist.

Although he is often well known for his dominance of logic and rigorous mathematical science, Von Neumann’s genius can be said to have grown from a comfortable and relaxed upbringing.

Early Life and Education in Budapest

He was born Neumann Janos on December 28, 1903, in Budapest, the capital of Hungary.  He was the first-born son of Neumann Miksa and Kann Margit.  In Hungarian, the family name appears before the given name.  So, in English, the parent’s names would be Max Neumann and Margaret Kann.  Max Neumann purchased a title early in his son’s life, and so became Von Neumann.

Max Neumann, born 1870, arrived in Budapest in the late 1880s.  He was a non-practicing Hungarian Jew with a good education.  He became a doctor of laws and then worked as a lawyer for a bank.  He had a good marriage to Margaret, who came from a prosperous family.

In 1903, Budapest was growing rapidly, a booming, intellectual capital.  It is said that the Budapest that Von Neumann was born into into “was about to produce one of the most glittering single generations of scientists, writers, artists, musicians, and useful expatriate millionaires to come from one small community since the city-states of the Italian Renaissance.^[1]”  Indeed, John Von Neumann was one of those who, through his natural genius and prosperous family, was able to excel in the elitist educational system of the time.

At a very young age, Von Neumann was interested in math, the nature of numbers and the logic of the world around him.  Even at age six, when his mother once stared aimlessly in front of her, he asked, “What are you calculating?” thus displaying his natural affinity for numbers.  The young Von Neumann was not only interested in math, though.  Just as in his adult life he would claim fame in a wide range of disciplines (and be declared a genius in each one), he also had varying interests as a child.  At age eight he became fascinated by history and read all forty-four volumes of the universal history, which resided in the family’s library.  Even this early, Von Neumann showed that he was comfortable applying his mind to both the logical and social world.

His parents encouraged him in every interest, but were careful not to push their young son, as many parents are apt to do when they find they have a genius for a child.  This allowed Von Neumann to develop not only a powerful intellect but what many people considered a likable personality as well.

It was never in question that Von Neumann would attend university, and in 1914, at the age of 10, the educational road to the university started at the Lutheran Gymnasium.  This was one of the three best institutions of its kind in Budapest at the time and gave Von Neumann the opportunity to develop his great intellect.  Before he would graduate from this high school he would be considered a colleague by most of the university mathematicians.  His first paper was published in 1922, when he was 17, in the Journal of the German Mathematical Society, dealing with the zeros of certain minimal polynomials.

University — Berlin, Zurich and Budapest

;In 1921 Von Neumann was sent to become a chemical engineer at the University of Berlin and then to Zurich two years later.  Though John Von Neumann had little interest in either chemistry or engineering, his father was a practical man and encouraged this path.  At that time chemical engineering was a popular career that almost guaranteed a good living,  in part due to the success of German chemists from 1914 to 1918.  So, Von Neumann set on the road planned in part by his father Max.  He would spend two years in Berlin in a non-degree chemistry program.  After this, he would take the entrance exam for second year standing in the chemical engineering program at the prestigious Eidgennossische Technische Hochschule (ETH) in Zurich, where Albert Einstein had failed the entrance exam in 1895 and then gained acceptance a year later.

During this time of practical undergraduate study, Von Neumann was executing another plan that was more in tune with his interests.  In the summer after his studies at Berlin and before he went to Zurich he enrolled at the Budapest University as a candidate for an advanced doctorate in mathematics.  His Ph.D. thesis was to attempt the axiomatization of set theory, developed by George Cantor.  At the time, this was one of the hot topics in mathematics and had already been studied by great professors, causing a great deal of trouble to most of them.  None-the-less, the young Von Neumann, devising and executing this plan at the age of 17, was not one to shy away from great intellectual challenges.

Von Neumann breezed through his two years at Berlin and then set himself to the work on chemical engineering at the ETH and his mathematical studies in Budapest.  He received excellent grades at the ETH, even for classes he almost never attended.  He received a perfect mark of 6 in each of his courses during his first semester in the winter of 1923 - 1924; courses including organic chemistry, inorganic chemistry, analytical chemistry, experimental physics, higher mathematics and French language.

From time to time he would visit Budapest University when his studies there required his presence and to visit his family.  He worked on his set theory thesis in Zurich while completing classes for the ETH.  After finishing his thesis he took the final exams in Budapest to receive his Ph.D. with highest honors.  This was just after his graduation from the ETH, so in 1926 he had two degrees, one an undergraduate degree in chemical engineering and the other a Ph.D. in mathematics, all by the time he was 22 years old.

Quantum Mechanics

Von Neumann was a creative and original thinker, but he also had the ability to take other people’s suggestions and concepts and in short order turn them into something much more complete and logical.  This is in a way what he did with quantum mechanics after he went to the university in Göttingen, Germany after receiving his degrees in 1926.

Quantum mechanics deals with the nature of atomic particles and the laws that govern their actions.  Theories of quantum mechanics began to appear to confront the discrepancies that occurred when one used purely Newtonian physics to describe the observations of atomic particles.

One of these observations has to do with the wavelengths of light that atoms can absorb and emit.  For example, hydrogen atoms absorb energy at 656.3 nanometers (nm), 486.1 nm, 434.0 nm or 410.2 nm, but not the wavelengths in between.  This was contrary to the principles of physics as they were at the end of the nineteenth century, which would predict that an electron orbiting the nucleus in an atom should radiate all wavelengths of light, therefore losing energy and quickly falling into the nucleus.  This is obviously not what is observed, so Berliner Max Planck introduced a new theory of quanta in 1900 that said energy could only be emitted in certain definable packets.

Two competing theories describing the nature of the atom, which could only absorb and emit energy in specific quanta, was the result of Max Planck’s theory.  One of these, developed by Erwin Schrödinger, suggested that the electron in hydrogen is analogous to a string in a musical instrument.  Like a string, which emits a specific tone along with overtones, the electron would have a certain “tone” at which it would emit energy.  Using this theory, Schrödinger developed a wave equation for the electron that correctly predicted the wavelengths of light that hydrogen would emit.

Another theory, developed by physicists at Göttingen including Werner Heisenberg, Max Born, and Pascual Jordan, focused on the position and momentum of an electron in an atom. They contested that these values were not directly observable (only the light emitted by the atom could be observed) and so could behave much differently from the motion of a particle in Newtonian physics. They theorized that the values of position and momentum should be described by mathematical constructs other than ordinary numbers.  The calculations they used to describe the motion of the electron made use of matrices and matrix algebra.

These two systems, although apparently very different, were quickly determined to be mathematically equivalent, two forms of the same principle.  The proponents of the two systems, none-the-less, denounced the others theories and claimed their own to be superior.  It is in this environment, in 1926, that Von Neumann appears on the scene and quickly went to work reconciling and advancing the theories of quantum mechanics.

Von Neumann wanted to find what the two systems, wave mechanics and matrix mechanics, had in common.  Through a more rigorous mathematical approach he wanted to find a new theory, more fundamental and powerful than the other two. He abstracted the two systems using an axiomatic approach, in which each logical state is the definite consequence of the previous state.  Von Neumann constructed the rules of “abstract Hilbert space” to aid in his development of a mathematical structure for quantum theory. His formalism of the subject allowed considerable advances to be made by others and even predicted strange new consequences, one that consciousness and observations alone can affect electrons in the laboratory.^[2]

Marriages and America

From 1927 to 1929, after his formalization of quantum mechanics, Von Neumann traveled extensively to various academic conferences and colloquia and turned out mathematical papers at the rate of one a month at times.  By the end of 1929 he had 32 papers to his name, all of them in German, and each written in a highly logical and orderly manner so that other mathematicians could easily incorporate Von Neumann’s ideas into their own work.

Von Neumann was now a rising star in the academic world, lecturing on new ideas, assisting other great minds of the time with their own works, and creating an image for himself as a likable and witty young genius in his early twenties.  He would often avoid arguments with the more confrontational of his colleagues by telling one of his many jokes or stories, some of which he could not tell in the presence of ladies (though there were few women at these mathematical seminars).  Other times he would bring up some interesting fact from ancient history, changing the subject and making Von Neumann seem surprisingly learned for his age and professional interests.

Near the end of 1929 he was offered a lectureship at Princeton in an America that was trying to stimulate its mathematical sciences by seeking out the best of Europe. At this same time, Von Neumann decided to marry Mariette Kovesi, whom he had known since his early childhood.  Their honeymoon was a cruise across the Atlantic to New York, although most of their trip was subdued by Mariette’s unexpected seasickness.

They had a daughter, Marina, in 1935. Von Neumann was affectionate with his new daughter, but did not contribute to the care of her or to the housework, which he considered to be the job of the wife.  The gap between the lively 26-year-old Mariette and the respectable 31-year-old John Von Neumann began to increase and in 1936 they broke up, Mariette going home to Budapest and Von Neumann, after drifting around Europe to various engagements, went to the United States.  Soon after, on a trip to Budapest, he met Klari Dan and they were married in 1938.

Although this marriage lasted longer than his first, Von Neumann was often distant from his personal life, obsessed and engrossed in his thoughts and work.  In this personal tradeoff of Von Neumann’s the world of science profited tremendously, and much of his work changed all of our lives.  Two of the most influential and well known of Von Neumann’s interests during his time in America, from 1933 (when he was appointed as one of the few original members of the Institute for Advanced Studies at Princeton) to 1957 (when he died of cancer), were the development of nuclear weapons and the invention of the modern digital computer.

Von Neumann’s Role in Nuclear Development

In the biography of a genius such as Von Neumann it would be easy to overestimate his role in the development of nuclear weapons in Los Alamos in 1943.  It is important to remember that there was a collection of great minds there, recruited by the American government to produce what many saw as a necessary evil.  The fear that Germany would produce an atomic bomb before the US drove the effort at Los Alamos.

Von Neumann’s two main contributions to the Los Alamos project were the mathematicization of development and his contributions to the implosion bomb.^[3]

The scientists at Los Alamos were used to doing scientific experiments but it’s difficult to do many experiments when developing weapons of mass destruction.  They needed some way to predict what was going to happen in these complex reactions without actually performing them.  Von Neumann therefore was a member of the team that invented modern mathematical modeling.  He applied his math skills at every level, from helping upper officials to make logical decisions to knocking down tough calculations for those at the bottom of the ladder.

The atomic bombs that were eventually dropped were of two kinds, one using Uranium-235 as its fissionable material, the other using Plutonium.  An atomic chain reaction occurs when the fissile material present in the bomb reaches a critical mass, or density.  In the Uranium-235 bomb, this was done using the gun method.  A large mass of Uranium-235, still under the critical mass, would have another mass of Uranium-235 shot into a cavity.  The combined masses would then reach critical mass, where an uncontrolled nuclear fission reaction would occur.  This process was known to work and was a relatively simple procedure.  The difficult part was obtaining the Uranium-235, which has to be separated from other isotopes of Uranium, which are chemically identical.  Plutonium, on the other hand, can be separated using chemical means, and so production of Plutonium based bombs could progress more quickly.  The problem here was that Plutonium bombs could not use the gun method.  The Plutonium would need to reach critical mass through another technique, implosion.  Here, a mass of Plutonium is completely surrounded by high explosives that are ignited simultaneously to cause the Plutonium mass to compress to supercritical levels and explode.

Although Von Neumann did not arrive first at the implosion technique for Plutonium, he was the one who made it work, developing the “implosion lens” of high explosives that would correctly compress the Plutonium.  This is just one more example of Von Neumann’s ability to pick up an idea and advance it where others had gotten stuck.

Development of Modern Computing

Just like the project at Los Alamos, the development of the modern computer was a collaborative effort including the ideas and effort of many great scientists.  Also like the development of nuclear weaponry, there have been many volumes written about the development of modern computer.  With so much involved in the process and Von Neumann himself being involved in so much of it, only a few contributions can be covered here.

Von Neumann’s experience with mathematical modeling at Los Alamos, and the computational tools he used there, gave him the experience he needed to push the development of the computer.  Also, because of his far reaching and influential connections, through the IAS, Los Alamos, a number of Universities and his reputation as a mathematical genius, he was in a position to secure funding and resources to help develop the modern computer.  In 1947 this was a very difficult task because computing was not yet a respected science.  Most people saw computing only as making a bigger and faster calculator.  Von Neumann on the other hand saw bigger possibilities.

Von Neumann wanted computers to be put to use in all fields of science, bringing a more logical and precise nature to those fields as he had tried to do.  With his contributions to the architecture of the computer, which describe how logical operations are represented by numbers that can then be read and processed, many Von Neumann’s dreams have come true.  Today we have extremely powerful computing machines used in scores of scientific fields, as well many more non-scientific fields.

In Von Neumann’s later years, however, he worked and dreamed of applications for computers that have not yet been realized.  He drew from his many other interests and imagined powerful combinations of the computer’s ability to perform logically and quickly with our brain’s unique ability to solve ill-defined problems with little data, or life’s ability to self-reproduce and evolve.

In this vein, Von Neumann developed a theory of artificial automata.  Von Neumann believed that life was ultimately based on logic, and so any construct that supports logic should be able to support life.  Artificial automata, like their natural counter parts, process information and proceed in their actions based on data received from their environment in light of rules and instructions they hold internally. Cellular automata are a class of automata that exist in an infinite plane that is covered by square cells, much like a sheet of graph paper.  Each of these cells can rest in a number of states.  The whole plane of cells will go through time steps, where the new state of each cell is determined by its own state and the state of the cells neighboring it.  In these simple actions there lies a great complexity and the basis for life like actions.  Below is a schematic diagram of Von Neumann’s self-reproducing cellular automaton.^[4]

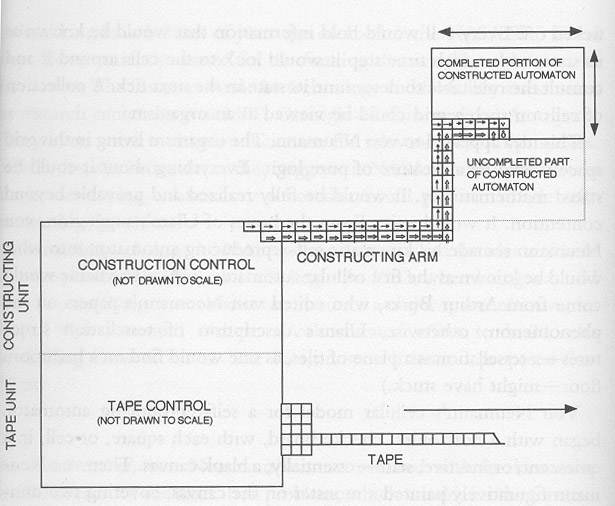
The automaton in this case, using the simple process described above, will produce an exact replica of itself, which can then reproduce on its own.  The cells in the tape change states in such a way as to propagate into the tape control unit of the automaton, which reacts by changing the state of the “steady” cells outside itself.  This constructs an arm that extends and forms a new automaton, exactly like the original.

Untimely End

Perhaps all deaths can be considered to come too early; John Von Neumann’s own death came far too early.  He died on February 8, 1957, 18 months after he was diagnosed with cancer.

He never finished his work on automata theory, although he worked as long as he possibly could.  He attended ceremonies held in his honor using a wheelchair, and tried to keep up appearances with his family and friends.  Though he had accomplished so much in his years he could not accept death, could not consider a world that existed without his mind constantly thinking and solving.  But today, his ideas live on and affect our lives in more ways than the few examples given here can demonstrate.

NOTES:

¹ Macrae, N., John Von Neumann; Pantheon: New York, NY, 1992. p 31

² Heims, S J., John Von Neumann and Norber Weiner; MIT Press: Cambridge, Massachusetts, 1980.

³ Macrae, N., John Von Neumann; Pantheon: New York, NY, 1992. p 234

⁴ Levy, S., Artificial Life; Pantheon: New York, NY, 1992. p 44

SHORT BIBLIOGRAPHY:

Aspray, William. 1990.  John Von Neuman and the Origins of Modern Computing.  Cambride, Mass.: MIT Press.

Aspray, William, and Arthur W. Burkes, eds. 1987.  Papers of John Von Neumann on Computing and Computer Theory.  Cambride, Mass.: MIT Press.

Heims, Steve J. 1980.  John Von Neumann and Norbert Wiener:  From Mathematics to the Technologies of Life and Death.  Cambride, Mass.: MIT Press.

Levy, Steven. 1992.  Artificial Life: A Report from the Frontier Where Computers Meet Biology.  New York, NY: Vintage Books.

Macrae, Norman. 1992.  John Von Neumann.  New York, NY: Pantheon.

Poundstone, William. 1992.  Prisoner’s Dilemma.  New York, NY: Doubleday.

FURTHER WEB RESOURCES:

http://ei.cs.vt.edu/~history/VonNeumann.html

http://www-groups.dcs.st-andrews.ac.uk/~history/References/Von_Neumann.html

Thanks to Daniel Kunkle for providing John Von Neumann's official biography.

HYPERLINKS:

Index and Direct Hyperlinks to the Other Web Pages on this Website:

AL BIELEK:

1. The Philadelphia Experiment and the Secrets of Montauk Home Page



2. Introduction



3. Life of Al Bielek



4. Timeline



5. Aliens, Time Travel, and Wormholes

THE PHILADELPHIA EXPERIMENT:

1. US Navy Official Record



2. The Philadelphia Experiment Story



3. The Philadelphia Experiment



4. Life of Ed Cameron



5. Dr. James Corum



6. Nikola Tesla



7. Dr. John Von Neumann - Official Record

THE MONTAUK PROJECT:

1. Camp Hero - Fort Montauk



2. Montauk Project



3. Larry James



4. Preston Nichols



5. Stewart Swerdlow



6. Duncan Cameron

© Copyright Al Bielek, June 24, 2004.
All rights reserved.  No portion of this document may be
reproduced in any form without written permission of the author.